DART

Overview

The Double Asteroid Redirection Test (DART) Mission was NASA and humanity’s first dedicated planetary defense mission. The mission was designed to be a technology demonstration of the kinetic impactor technique to deflect an asteroid. The target of the mission was the binary asteroid system Didymos, which consists of a primary body (Didymos) and a smaller secondary body (Dimorphos). The DART spacecraft was launched in November 2021 and successfully impacted Dimorphos in September 2022. The impact was observed by multiple ground and space-based observatories. Furthermore, the European Space Agency (ESA) will launch the Hera spacecraft in 2024 to characterize the changes in the binary system in detail. Together, NASA’s DART mission and ESA’s Hera mission form the Asteroid Impact & Deflection Assessment (AIDA) collaboration.

Artist’s impression of the DART spacecraft on course to impact Dimorphos (Credit: NASA/JHUAPL).

The Momentum Enhancement Factor

The momentum enhancement factor, $\beta$ is a measure of the efficiency of a kinetic impact at an asteroid. It is defined as the ratio of the momentum transferred to the asteroid to the momentum of the impactor. $\beta$ is a function of the impact velocity, the impact angle, and the asteroid’s bulk density. $\beta$ is a key parameter in studying the consequences of a kinetic impactor mission.

This is because for kinetic impacts, the momentum transfer is not simply a consequence of the impulse delivered by the impactor. Once the impactor hits the asteroid, a significant and non-negligible amount of material such as pebbles, boulders, and dust is ejected from the surface of the asteroid. Therefore, the initial momentum transfer from the impactor is augmented by the ejecta leaving the asteroid’s surface. The momentum enhancement factor ($\beta$) is a measure of this augmentation. $\beta$ is calculated using the following equation:

\[\beta = \frac{||(M/m) \Delta \boldsymbol{V} - \boldsymbol{V}_{\infty} + \left(\boldsymbol{V}_{\infty} \cdot \hat{\boldsymbol{n}}\right) \hat{\boldsymbol{n}}||}{||\left(\boldsymbol{V}_{\infty} \cdot \hat{\boldsymbol{n}}\right) \hat{\boldsymbol{n}}||}\]

where $M$ is the mass of the asteroid, $m$ is the mass of the impactor, $\Delta \boldsymbol{V}$ is the change in velocity of the asteroid, $\boldsymbol{V}_{\infty}$ is the relative velocity of the impactor with respect to the asteroid at impact, and $\hat{\boldsymbol{n}}$ is the unit vector normal to the surface of the asteroid at the impact point.

This equation is extremely complicated. However, to gain a better understanding of the momentum enhancement factor, we can simplify the equation by assuming that it is a head-on impact where the ejecta travels in the opposite direction of the impactor. In this case, the equation significantly simplifies to:

\[\beta = 1 + \frac{p_{\text{ejecta}}}{p_{\text{impactor}}}\]

where $p_{\text{ejecta}}$ is the momentum of the ejecta (in the direction opposite to the impactor) and $p_{\text{impactor}}$ is the momentum of the impactor at impact. This equation is much simpler and easier to understand. It simply states that $\beta-1$ is the ratio of the contribution of the ejecta to the momentum transfer to the momentum transferred by the impactor. For instance, if $\beta = 1$, then the ejecta does not contribute to the momentum transfer at all. If $\beta = 2$, then the ejecta contributes just as much to the momentum transfer as the impactor. If $\beta = 3$, then the ejecta contributes twice as much to the momentum transfer as the impactor, and so on.

Furthermore, for impacts at binary asteroids in general, there is a notion of the heliocentric momentum enhancement factor ($\beta_\odot$). This is because some of the material ejected from the asteroid may have a small enough velocity to stay trapped in the gravitational potential of the binary system. This material does not help in pushing the asteroid system away from the Earth in case it is being deflected using a kinetic impactor mission. Therefore, the heliocentric momentum enhancement factor ($\beta_\odot$) is defined using only the momentum that escapes the binary system’s gravitational influence.

My Work (Pre-impact)

Before the DART spacecraft impacted Dimorphos, I worked on a project to ensure that no achievable value of $\beta_\odot$ would put the Didymos system on a collision course with the Earth. This involved doing a systematic sweep of both reasonable and unreasonably high values of $\beta_\odot$ to study the future close approaches of the Didymos system with the Earth. The below figure shows the location of the Didymos system (and the corresponding 3-$\sigma$ ellipses) for different impact outcomes on the B-plane (if you are unfamiliar with the B-plane, check out this paper).

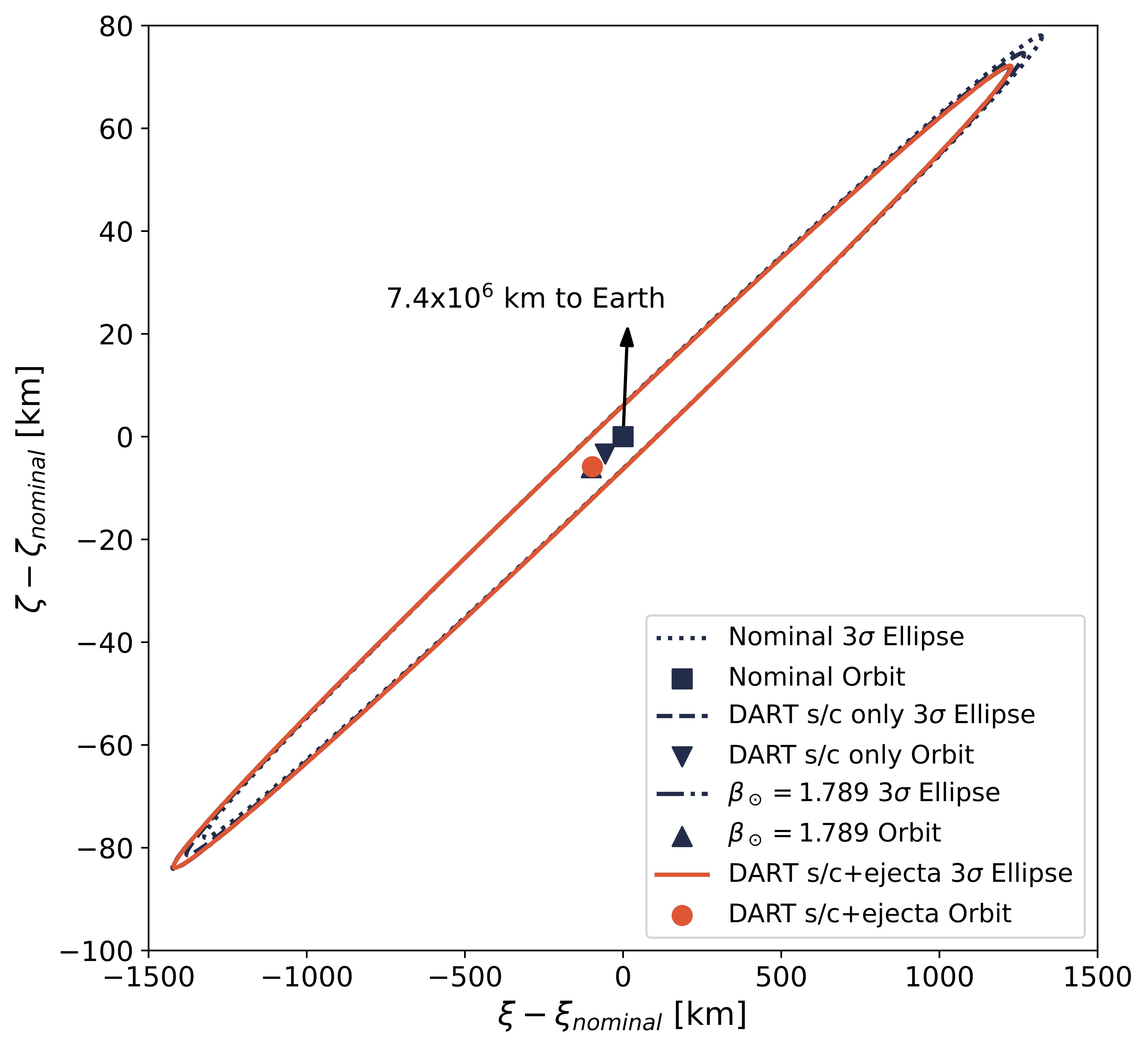
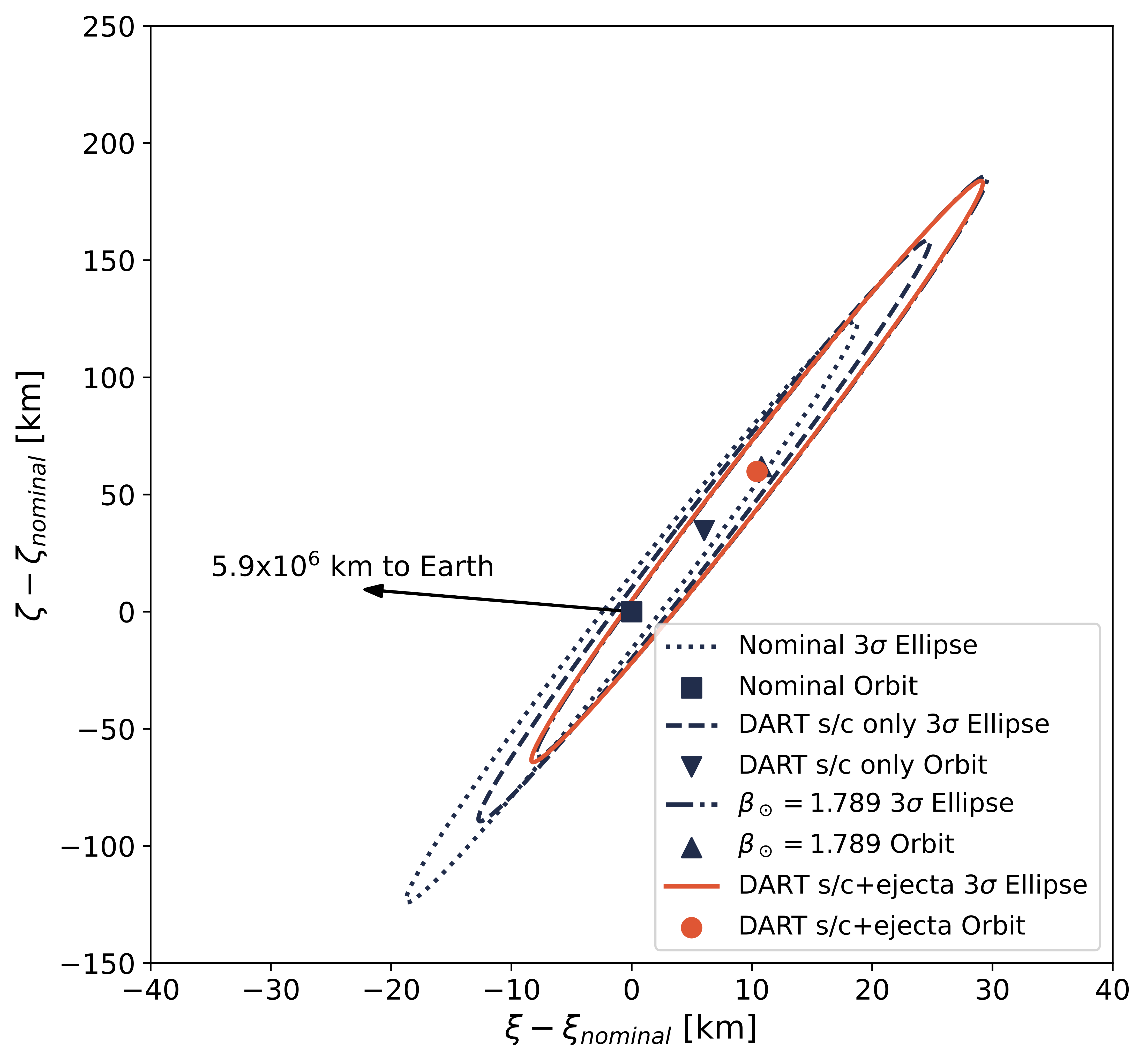B-plane uncertainty ellipses for varying heliocentric impact outcomes for the 2062 (left) and 2123 (right) close approaches.

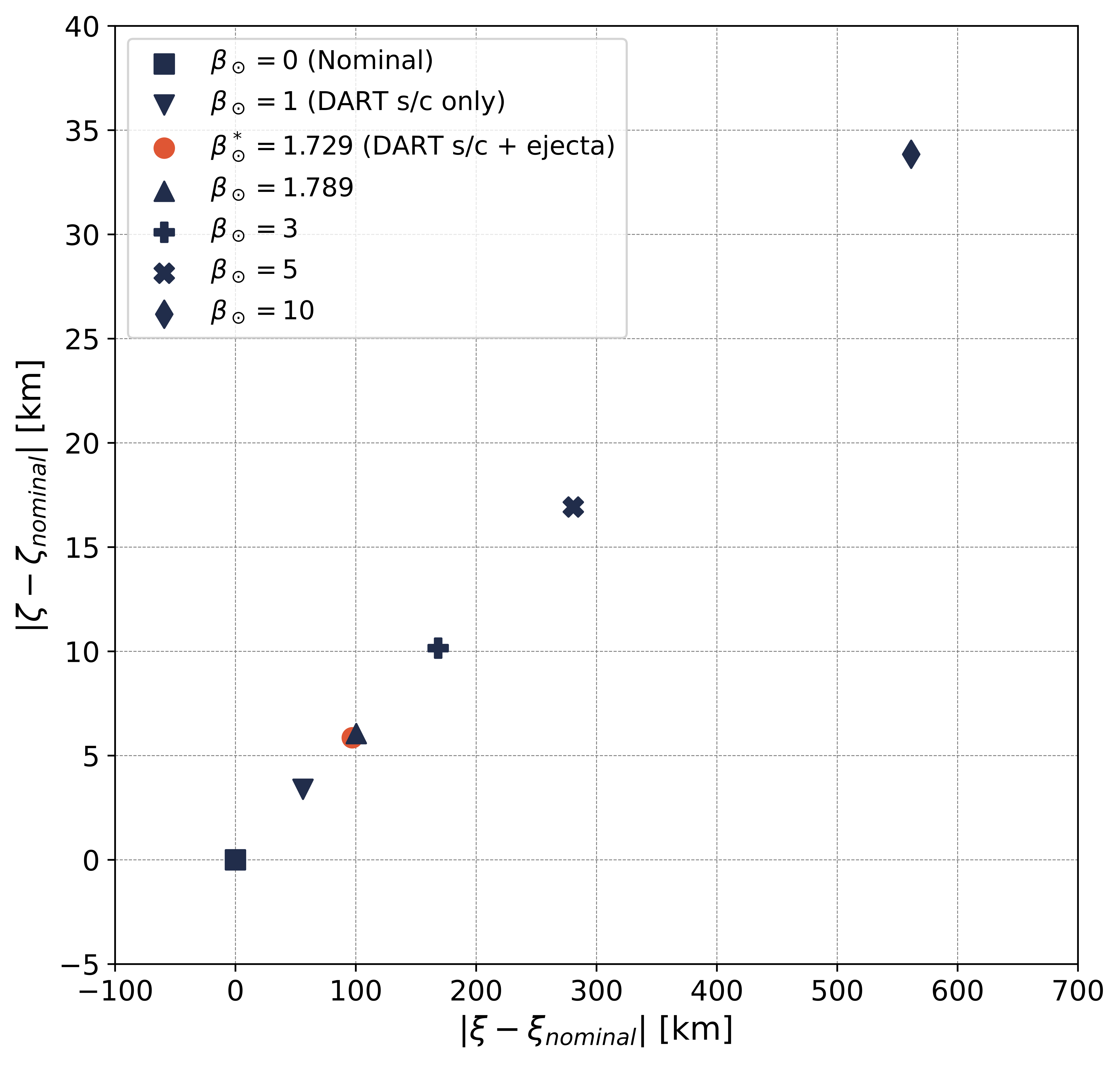
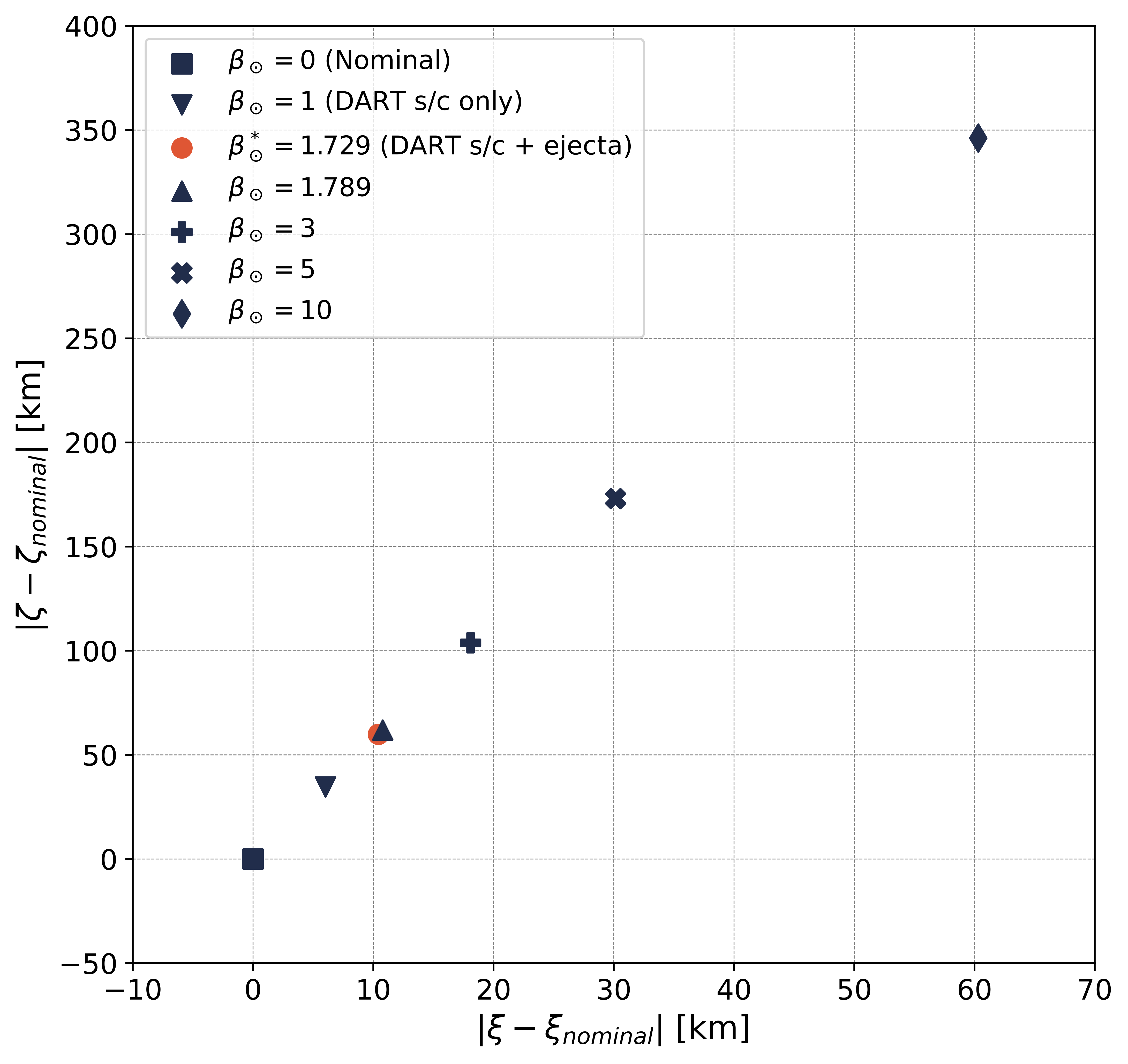B-plane locations for varying $\beta_\odot$ values for the 2062 (left) and 2123 (right) close approaches.

Additionally, the above figure shows the deflection of the Didymos system for different $\beta_\odot$ values. The deflection is measured in terms of the change in the Didymos system’s nominal B-plane location. Given that these close approaches happen millions of kilometers away from the Earth, and the deflection corresponding to an unrealistically high $\beta_\odot$ value of 10 is only a few hundred kilometers, we can safely say that the Didymos system will not be on a collision course with the Earth due to the DART experiment. For more details on this work, check out my pre-DART impact paper.

My Work (Post-impact)

Once we knew that the DART impact would not put the Didymos system on collision course with the Earth, We started working on how we could measure the exact value of $\beta_\odot$ using both pre- and post-impact observations. To do this we considered multiple observation scenarios and studied the Signal-to-Noise Ratio (SNR) of $\beta_\odot$ in each scenario. The below table shows the SNR of $\beta_\odot$ for four different observation scenarios.

Note—The target value to be retrieved in these simulations is $\beta_\odot=3$, $A_{\text{2}}=-1.04\times 10^{-14}$ au/day$^2$.

One key result we found from this work on measurability of $\beta_\odot$ is the high correlation between the $\beta_\odot$ estimate and the $A_{\text{2}}$ parameter. This $A_{\text{2}}$ parameter is a transverse nongravitational acceleration term that is used to model the Yarkovsky effect on an asteroid. The Yarkovsky effect is a phenomenon caused by the uneven heating of an asteroid by the Sun. This uneven heating causes the asteroid to emit more thermal radiation from the side that is facing away from the Sun. This causes a net force on the asteroid that can change its orbit over time. The $A_{\text{2}}$ parameter is a measure of this force. The below figure shows the $\beta_\odot$-$A_{\text{2}}$ estimate and associated uncertainty for the four observation scenarios. For more details on this work, see my post-DART impact paper.

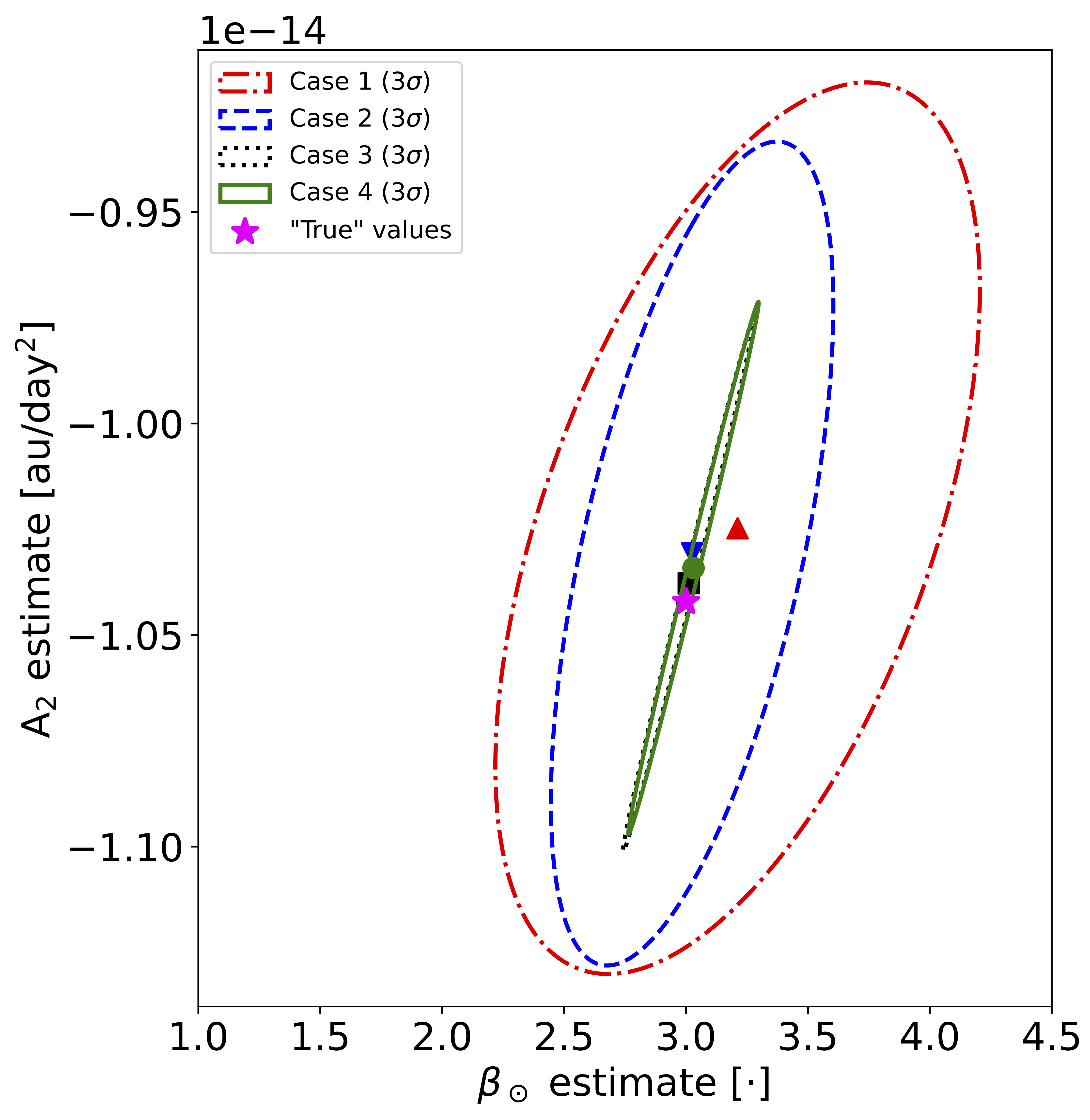
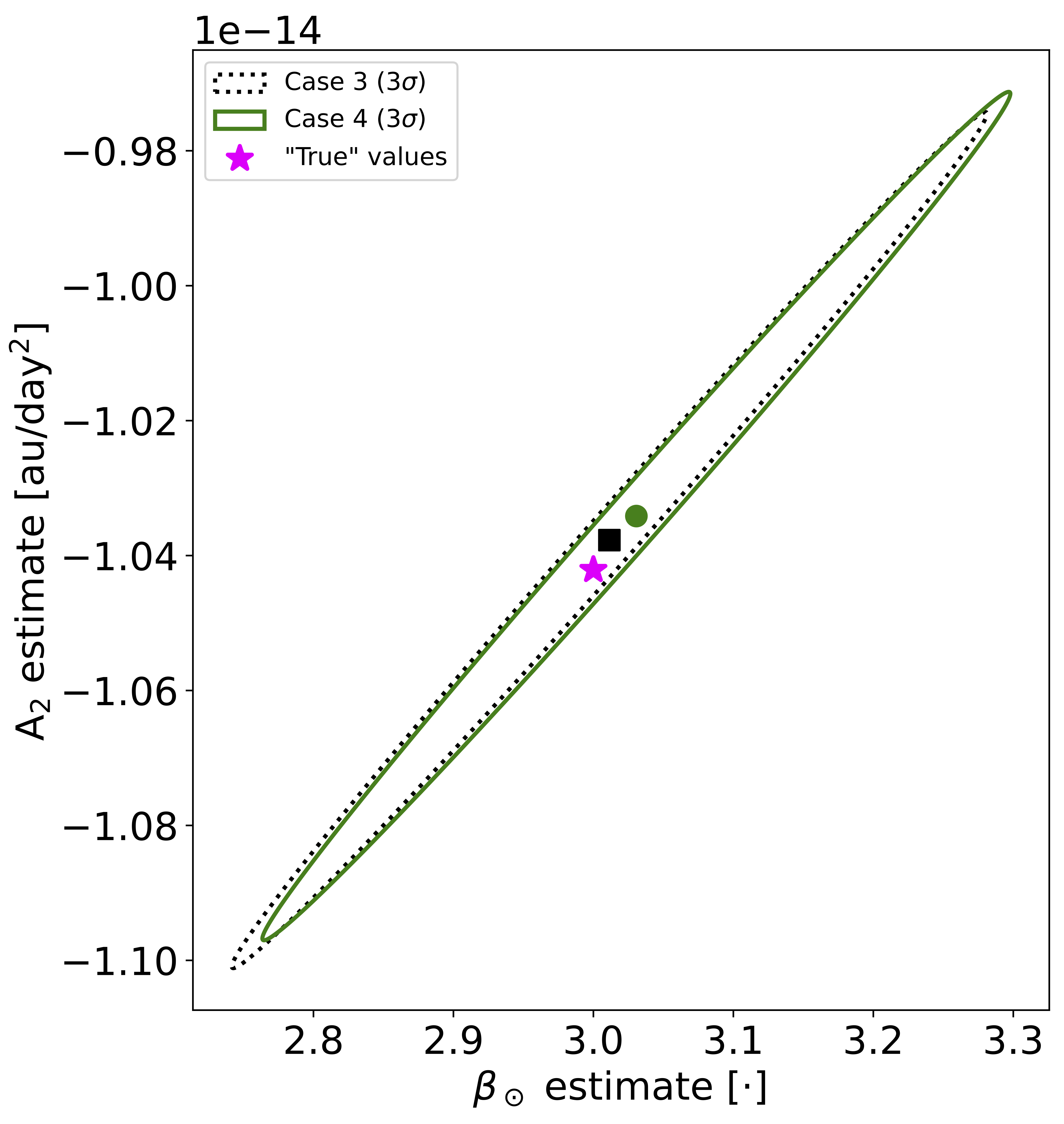$\beta_\odot$-$A_{\text{2}}$ covariance mapping for all four future observation scenarios considered in this work (left) and zoomed in view of Cases 3 and 4 (right).